Learning of manifolds

I will restructure learning on manifolds and dimensionality reduction into a more useful distinction.

As in — handling your high-dimensional, or graphical, data by trying to discover a low(er)-dimensional manifold that contains it. That is, inferring a hidden constraint that happens to have the form of a smooth surface of some low-ish dimension. Related: Learning on manifolds, and if you squint at it, learnable indexes.

There are a million different versions of this. Multidimensional scaling seems to be the oldest.

Tangential aside: in dynamical systems we talk about creating high-dimensional Takens embedding for state space reconstruction for arbitrary nonlinear dynamics. I imagine there are some connections between learning the lower-dimensional manifold upon which lies your data, and the higher-dimensional manifold in which your data’s state space is naturally expressed. But I would not be the first person to notice this, so hopefully it’s done for me somewhere?

See also kernel methods, and functional regression, which connects via diffusion maps (Ronald R. Coifman and Lafon 2006; R. R. Coifman et al. 2005, 2005).

See also information geometry, which uses manifolds also but one implied by the parameterisation of a parametric model.

To look at: ISOMAP, Locally linear embedding, spectral embeddings, diffusion maps, multidimensional scaling…

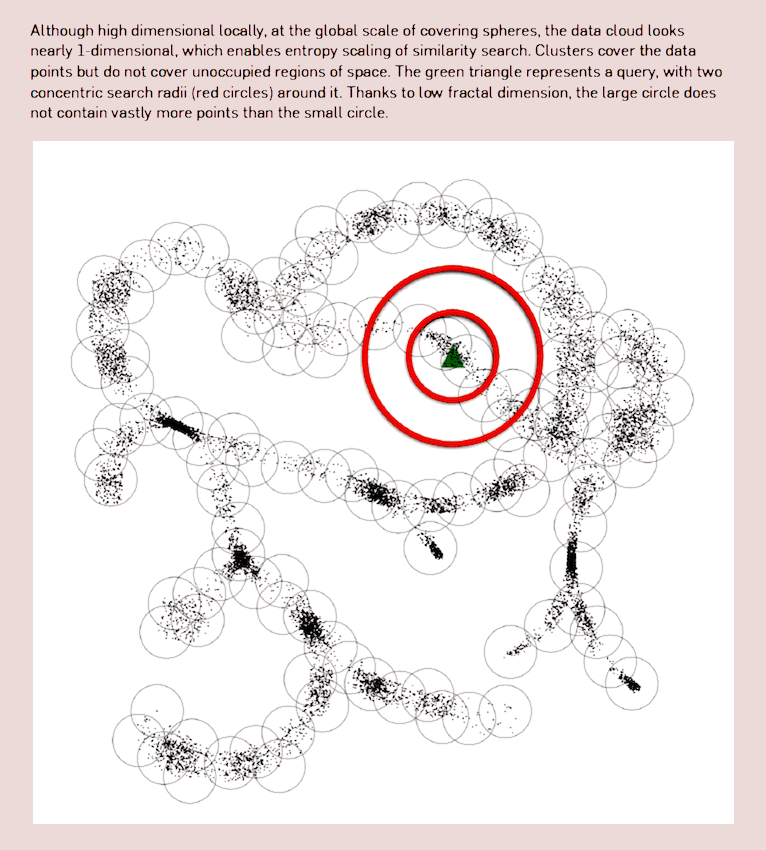
Bioinformatics is leading to some weird use of data manifolds; see for example Berger, Daniels, and Yu (2016) for the performance implications of knowing the manifold shape for *-omics search, using compressive manifold storage based on both fractal dimension and metric entropy concepts. Also suggestive connection with fitness landscape in evolution.

Neural networks have some implicit manifolds, if you squint right. See Christopher Olah’s visual explanation how, whose diagrams should be stolen by someone trying to explain V-C dimension.

Berger, Daniels, and Yu (2016) argue:

Manifold learning algorithms have recently played a crucial role in unsupervised learning tasks such as clustering and nonlinear dimensionality reduction […] Many such algorithms have been shown to be equivalent to Kernel PCA (KPCA) with data-dependent kernels, itself equivalent to performing classical multidimensional scaling (cMDS) in a high-dimensional feature space (Schölkopf et al., 1998; Williams, 2002; Bengio et al., 2004). […] Recently, it has been observed that the majority of manifold learning algorithms can be expressed as a regularized loss minimization of a reconstruction matrix, followed by a singular value truncation (Neufeld et al., 2012)