Multi-output Gaussian process regression

December 2, 2020 — November 26, 2021

Gaussian
Hilbert space
kernel tricks
regression
spatial
stochastic processes
time series
Figure 1

Multi-task learning in GP regression assumes the model is distributed as a multivariate Gaussian process.

WARNING: Under heavy construction ATM; and makes no sense.

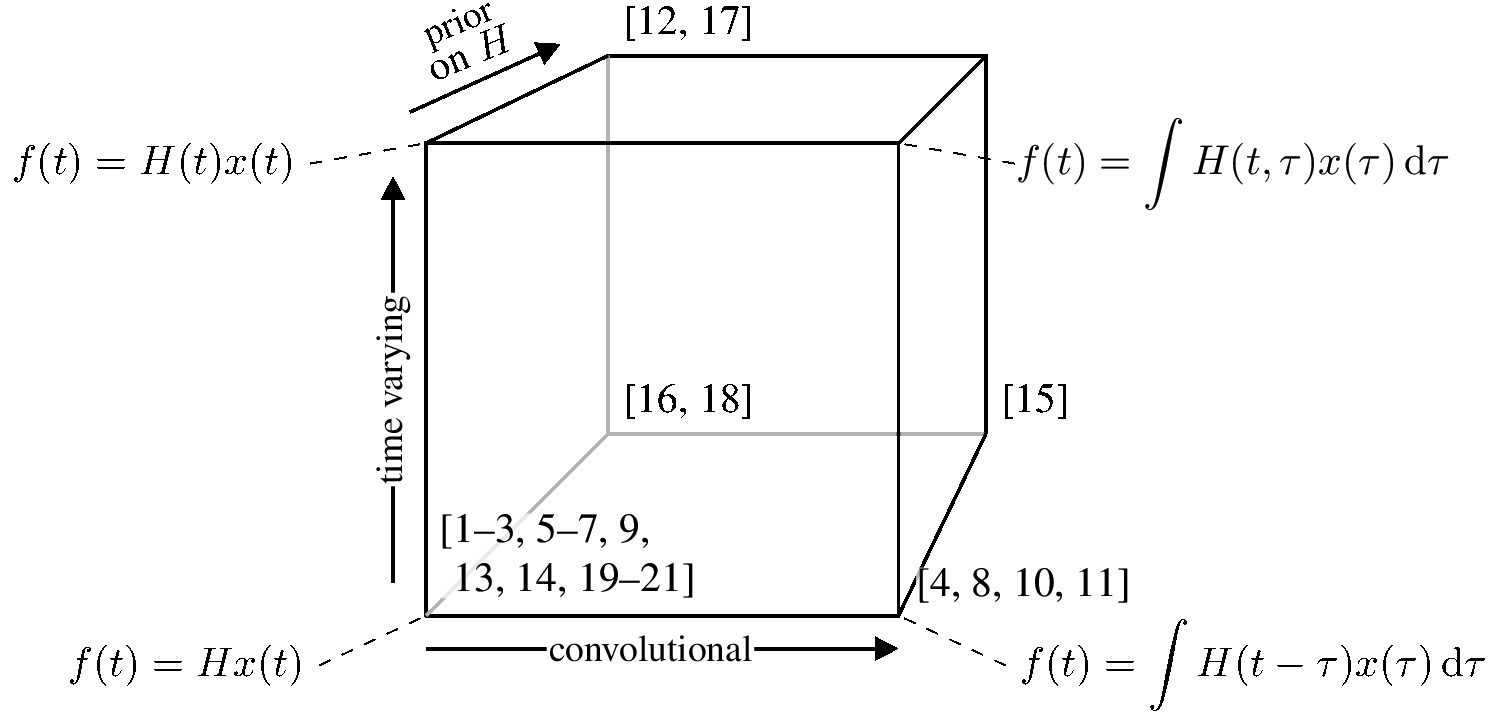
My favourite introduction is by Eric Perim, Wessel Bruinsma, and Will Tebbutt, in a series of blog posts spun off a paper (Bruinsma et al. 2020) which attempts to unify various approaches to defining vector GP processes, and thereby derive an efficient method incorporating good features of all of them. A unifying approach feels necessary; there is a lot of terminology going on.

Now that I have this tool I am going to summarize it for myself to get a better understanding. It will probably supplant some of the older material below, and maybe also some of the GP factoring material.

To define in their terms: Co-regionalization…

The essential insight is that in practice we probably assume a low-rank structure (to be defined) for the cross-covariance matrix, which will mean that it is some kind of linear mixing of scalar GPs. And there are only so many ways that can be done, as summarised in their diagram:

Figure 2: The Mixing Model Hierarchy summarises lots of approaches

We could of course assume non-linear mixing, but then we are doing some other things, perhaps variational autoencoding or Deep GPs.

1 Tooling

Most of the GP toolkits do multi-output as well.

Here is one with some interesting documentation.

This repository provides a toolkit to perform multi-output GP regression with kernels that are designed to utilize correlation information among channels in order to better model signals. The toolkit is mainly targeted to time-series, and includes plotting functions for the case of single input with multiple outputs (time series with several channels).

The main kernel corresponds to Multi Output Spectral Mixture Kernel, which correlates every pair of data points (irrespective of their channel of origin) to model the signals. This kernel is specified in detail in Parra and Tobar (2017).

2 References

Adler, Robert J., and Taylor. 2007. Random Fields and Geometry. Springer Monographs in Mathematics 115.
Adler, Robert J, Taylor, and Worsley. 2016. Applications of Random Fields and Geometry Draft.
Álvarez, and Lawrence. 2011. “Computationally Efficient Convolved Multiple Output Gaussian Processes.” Journal of Machine Learning Research.
Álvarez, Rosasco, and Lawrence. 2012. “Kernels for Vector-Valued Functions: A Review.” Foundations and Trends® in Machine Learning.
Bonilla, Chai, and Williams. 2007. “Multi-Task Gaussian Process Prediction.” In Proceedings of the 20th International Conference on Neural Information Processing Systems. NIPS’07.
Bruinsma, Perim, Tebbutt, et al. 2020. “Scalable Exact Inference in Multi-Output Gaussian Processes.” In International Conference on Machine Learning.
Dai, Álvarez, and Lawrence. 2017. “Efficient Modeling of Latent Information in Supervised Learning Using Gaussian Processes.” Advances in Neural Information Processing Systems.
Davison, and Ortiz. 2019. “FutureMapping 2: Gaussian Belief Propagation for Spatial AI.” arXiv:1910.14139 [Cs].
Evgeniou, Micchelli, and Pontil. 2005. “Learning Multiple Tasks with Kernel Methods.” Journal of Machine Learning Research.
Evgeniou, and Pontil. 2004. “Regularized Multi-Task Learning.” In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’04.
Gelfand, and Banerjee. 2010. “Multivariate Spatial Process Models.” In Handbook of Spatial Statistics.
Gneiting, Kleiber, and Schlather. 2010. “Matérn Cross-Covariance Functions for Multivariate Random Fields.” Journal of the American Statistical Association.
Leibfried, Dutordoir, John, et al. 2022. “A Tutorial on Sparse Gaussian Processes and Variational Inference.”
Lu. 2022. “A Rigorous Introduction to Linear Models.”
Micchelli, and Pontil. 2005a. “Learning the Kernel Function via Regularization.” Journal of Machine Learning Research.
———. 2005b. “On Learning Vector-Valued Functions.” Neural Computation.
Moreno-Muñoz, Artés, and Álvarez. 2018. “Heterogeneous Multi-Output Gaussian Process Prediction.” In Advances in Neural Information Processing Systems.
Moreno-Muñoz, Artés-Rodríguez, and Álvarez. 2019. “Continual Multi-Task Gaussian Processes.” arXiv:1911.00002 [Cs, Stat].
Osborne, Roberts, Rogers, et al. 2008. “Towards Real-Time Information Processing of Sensor Network Data Using Computationally Efficient Multi-Output Gaussian Processes.” In 2008 International Conference on Information Processing in Sensor Networks (Ipsn 2008).
Parra, and Tobar. 2017. “Spectral Mixture Kernels for Multi-Output Gaussian Processes.” In Advances in Neural Information Processing Systems.
Schlather, Malinowski, Menck, et al. 2015. “Analysis, Simulation and Prediction of Multivariate Random Fields with Package Random Fields.” Journal of Statistical Software.
Seeger, Teh, and Jordan. 2005. “Semiparametric Latent Factor Models.”
Stegle, Lippert, Mooij, et al. 2011. “Efficient Inference in Matrix-Variate Gaussian Models with Iid Observation Noise.” In Proceedings of the 24th International Conference on Neural Information Processing Systems. NIPS’11.
Williams, Klanke, Vijayakumar, et al. 2009. “Multi-Task Gaussian Process Learning of Robot Inverse Dynamics.” In Advances in Neural Information Processing Systems 21.